耀唐解读
在ABAQUS 中阻尼可以应用在下面的动力学分析中:
1、非线性问题直接积分求解(显式分析或者隐式分析);
2、直接法或子空间法稳态动力学分析;
3、模态动力学分析(线性)。
针对模态动力学分析,在ABAQUS/Standard 中可定义几种不同类型的阻尼:直接模态阻尼(Direct Modal Damping),瑞利阻尼(Rayleigh Damping),复合模态阻尼(Composite Modal Damping)和结构阻尼(Structure Damping)。
ABAQUS 模态动力学分析中用*MODAL DAMPING 选项来定义阻尼。阻尼是包含在分析步内定义的一部分,每阶模态可以定义不同量值的阻尼。
对应的ABAQUS 输入文件为: *MODAL DAMPING, MODAL=DIRECT 其中,*MODAL DAMPING 选项中的MODAL=DIRECT 参数表示被指定的直接模态阻尼,数据行输入的数据m1 为起始模态序号,m2 为截止模态序号,ξa 为模态阻尼比。 例如,对于前10 阶振型的阻尼定义为4%的临界模态阻尼,11~20 阶振型的阻尼为5%的临界阻尼,在分析步骤中的定义如下: *MODAL DAMPING, MODAL=DIRECT 其中,α和β是用户根据材料特性定义的常数。尽管假设阻尼正比于质量和刚度没有严格的物理基础,但是实际上我们对于阻尼分布的真实情况知之甚少,也就不能保证其它更为复杂的模型是正确的。通常,瑞利阻尼模型对于大阻尼系统,即阻尼值超过10%临界阻尼时是不可靠的。 使用瑞利阻尼有许多方便,例如系统的特征频率与对应的无阻尼系统特征值一致;相对于其它形式的阻尼,可以精确地定义系统每阶模态的瑞利阻尼;各阶模态的瑞利阻尼可转换为直接模态阻尼,在ABAQUS/Standard 中将瑞利阻尼转换为直接模态阻尼进行动力学计算。 其中ωi 表示第i 阶模态的固有频率。(2)式表明,瑞利阻尼的质量比例阻尼部分在系统响应的低频段起主导作用,刚度比例阻尼部分在高频段起主导作用。 对应的ABAQUS 文件输入为: *MODAL DAMPING, RAYLEIGH 参数RAYLEIGH指定阻尼形式为瑞利阻尼,m1、m2 的含义与直接模态阻尼定义相同。α、β分别为模态质量、刚度比例系数。例如,对前10 阶模态定义α=0.2525 和β=2.9×10−3,对于11~20 阶振型定义α= 0.2727 和β=3.03×10−3,则可以在分析步骤中定义: *MODAL DAMPING, RAYLEIGH 在复合阻尼中,对应于每种材料的阻尼定义一个临界阻尼比,这样就得到了对应于整体结构的复合阻尼值。如果结构由多种材料组成,那么采用复合阻尼来描述系统的阻尼特性是非常简便有效的。 其中,ξa 为模态α的模态阻尼比,ξm 材料m 的阻尼比, Mm M N 为与材料m相关的质量矩阵, φαM 为模态α的振型, ma 为模态的α模态质量。 在ABAQUS 中分两步定义复合阻尼。 对应的ABAQUS 输入文件为: *MATERIAL, NAME=STEEL 第二步,在分析步骤中引用复合阻尼,如图4 所示。 对应的ABAQUS 文件输入为: *STEP 系统的结构阻尼特性与结构或者材料的内摩擦机理有关。其他形式的阻尼属于粘性阻尼,即阻尼力的大小与运动速度成正比,而结构阻尼力与位移成正比。同时结构阻尼力不会随着激振频率变化而变化。 其中,FD 阻尼力,s 结构阻尼因子,I 是结构的变形力,i 虚数单位。 图5 对应ABAQUS 输入文件为: *MODAL DAMPING, STRUCTURAL 参数STRUCTURAL 指定模态阻尼形式为结构阻尼。m1、m2 的含义与定义直接模态阻尼相同,s 为结构阻尼因子。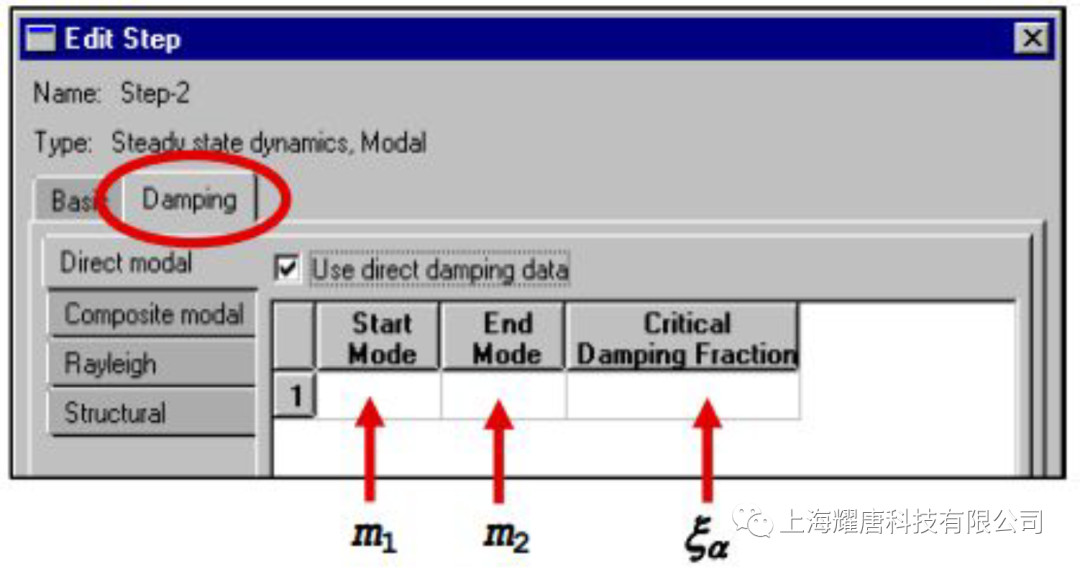
m1, m2, ξa
1,10,0.04
11,20,0.05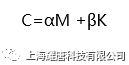
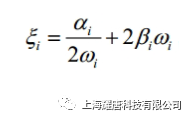
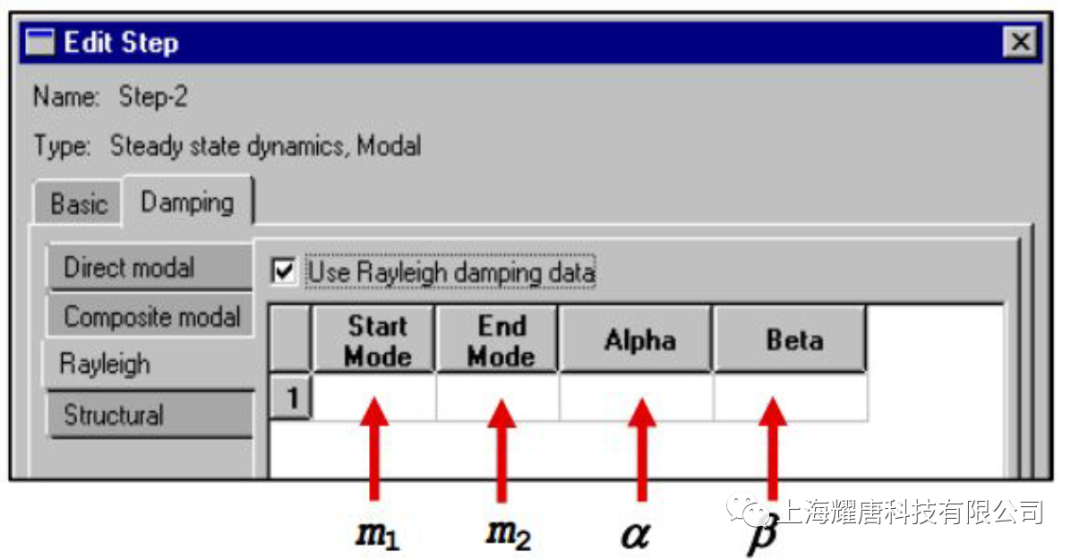
m1, m2, α,β
1,10,0.2525,2.9E-3
11,20,0.2727,3.03E-3

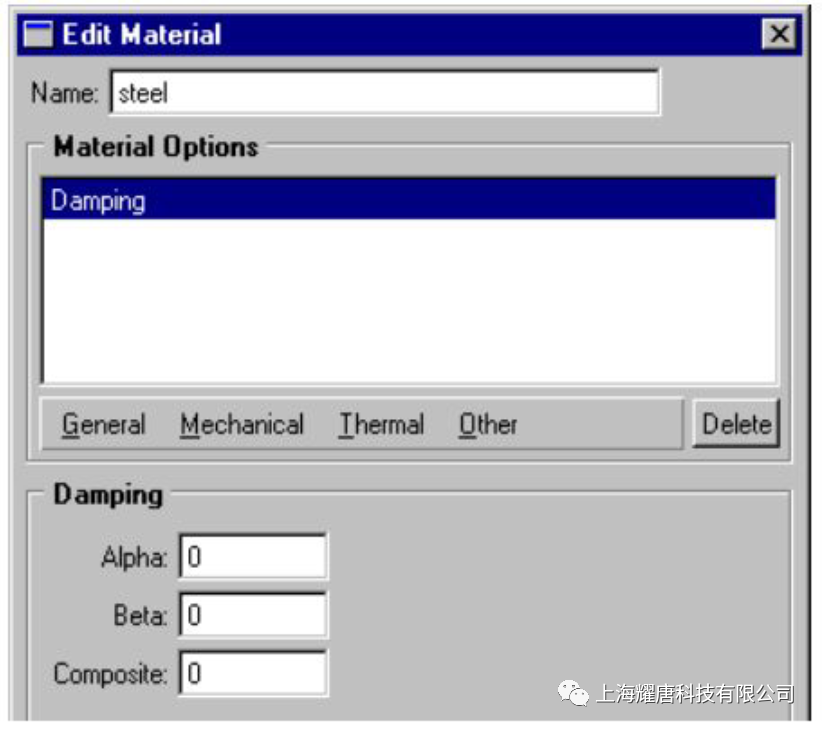
*DAMPING, COMPOSITE=ξM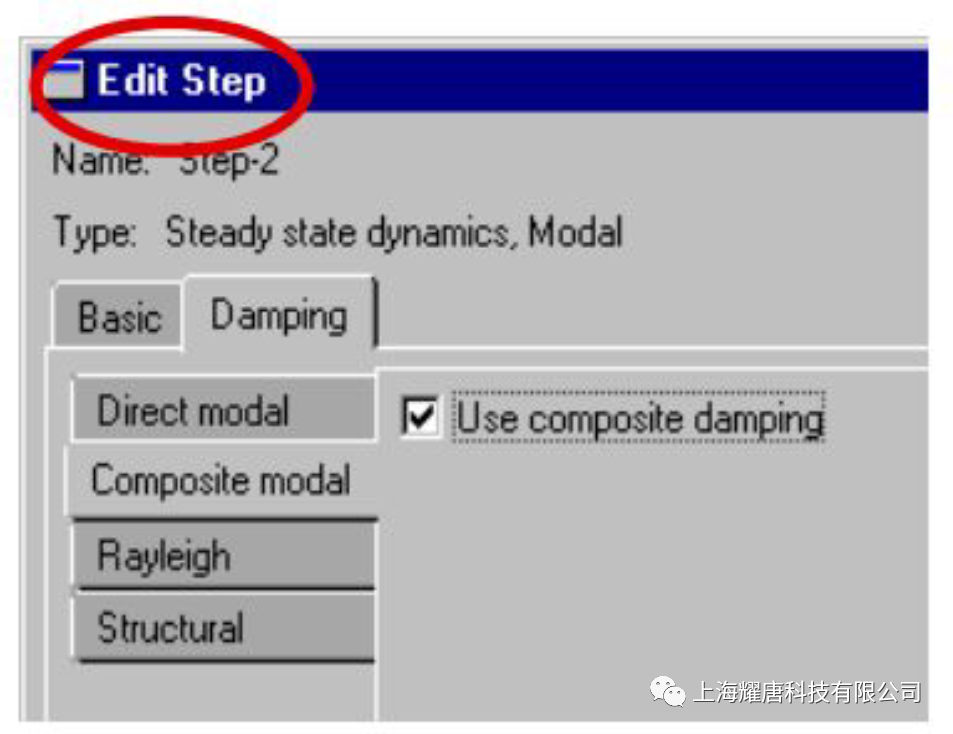
……
*MODAL DAMPING, MODAL=COMPOSITE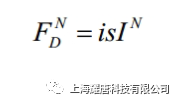
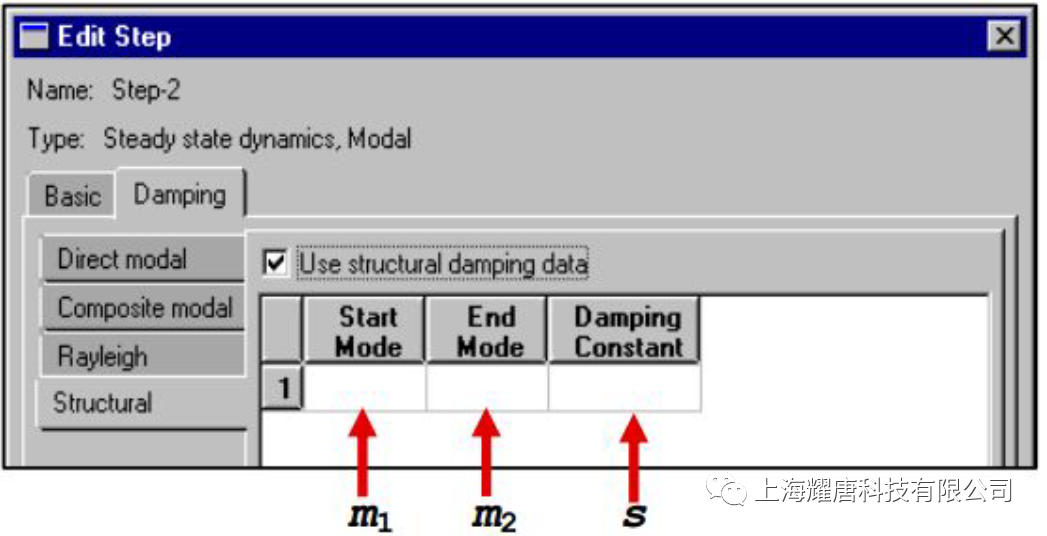
m1, m2, s